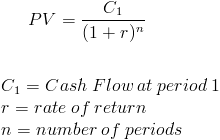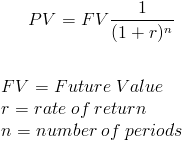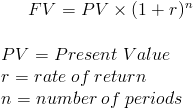Present Value

Click here for original document.

 

Present Value (PV) is a formula used in Finance that calculates the present day value of an amount that is received at a future date. The premise of the equation is that there is "time value of money".

Time value of money is the concept that receiving something today is worth more than receiving the same item at a future date. The presumption is that it is preferable to receive $100 today than it is to receive the same amount one year from today, but what if the choice is between $100 present day or $106 a year from today? A formula is needed to provide a quantifiable comparison between an amount today and an amount at a future time, in terms of its present day value.

 

Watch Video Tutorial One - Introduction to Present Value

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Use of Present Value Formula

 

The Present Value formula has a broad range of uses and may be applied to various areas of finance including corporate finance, banking finance, and investment finance. Apart from the various areas of finance that present value analysis is used, the formula is also used as a component of other financial formulas.

 

Watch Video Tutorial Two - Introduction to Present Value

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Example of Present Value Formula

 

An individual wishes to determine how much money she would need to put into her money market account to have $100 one year today if she is earning 5% interest on her account, simple interest.

The $100 she would like one year from present day denotes the C1 portion of the formula, 5% would be r, and the number of periods would simply be 1.

 

Putting this into the formula, we would have

 

PV = $100/1.05

 

 

When we solve for PV, she would need $95.24 today in order to reach $100 one year from now at a rate of 5% simple interest.

Alternative Formula

 

 

 

 

 

 

The Present Value formula may sometimes be shown as

 

 

 

 

Watch Video Tutorial Three - Introduction to Present Value

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Before you move-on to the final video tutorial, visit this site for additional reading materials.

 

 

 

Watch Video Tutorial Four - Introduction to Present Value

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Future Value

 

Future Value (FV) is a formula used in finance to calculate the value of a cash flow at a later date than originally received. This idea that an amount today is worth a different amount than at a future time is based on the time value of money.

 

The time value of money is the concept that an amount received earlier is worth more than if the same amount is received at a later time. For example, if one was offered $100 today or $100 five years from now, the idea is that it is better to receive this amount today. The opportunity cost for not having this amount in an investment or savings is quantified using the future value formula. If one wanted to determine what amount they would like to receive one year from now in lieu of receiving $100 today, the individual would use the future value formula.

 

The future value formula also looks at the effect of compounding. Earning .5% per month is not the same as earning 6% per year, assuming that the monthly earnings are reinvested. As the months continue along, the next month's earnings will make additional monies on the earnings from the prior months. For example, if one earns interest of $40 in month one, the next month will earn interest on the original balance plus the $40 from the previous month. This is known as compound interest.

 

Watch Video Tutorial Five - Compound Interest - Future Value

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Use of Future Value

 

The future value formula is used in essentially all areas of finance. In many circumstances, the future value formula is incorporated into other formulas. As one example, an annuity in the form of regular deposits in an interest account would be the sum of the future value of each deposit. Banking, investments, corporate finance all may use the future value formula is some fashion.

 

 

Example of Future Value Formula

An individual would like to determine their ending balance after one year on an account that earns .5% per month and is compounded monthly. The original balance on the account is $1000. For this example, the original balance, which can also be referred to as initial cash flow or present value, would be $1000, r would be .005(.5%), and n would be 12 (months).

Putting this into the formula, we would have:

 

 

 

After solving, the ending balance after 12 months would be $1061.68.

 

As a side note, notice that 6% of $1000 is $60. The additional $1.68 earned in this example is due to compounding.

 

Alternative Formula

 

The Future Value formula may also be shown as

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

 

 

 

 

Course Work Number 1

Complete the following questions.  Show each step taken while solving the problem and then upload your answer in the assignment submission box.  This values 10%. Due no later than February 8, 2015.

 

 

 

1. What is the present value of an offer of $15,000 one year from now if the opportunity cost of capital (discount rate) is 12% per year simple interest?

 

 

2. What is the present value of an offer of $14,000 one year from now if the opportunity cost of capital (discount rate) is 11% per year simple interest?

 

3. What is the present value of an offer of $15,000 two years from now if the opportunity cost of capital (discount rate) is 12% per year compounded annually?

 

 

4. What is the present value of an offer of $14,000 two years from now if the opportunity cost of capital (discount rate) is 11% per year compounded annually?

 

5. What is the future value of $20,000 that grows at an annual interest rate of 12% per year for two years?

 

6. What is the future value of $25,000 which grows at an annual interest rate of 11% per year for two years?

 

 

7. What is the present value of an offer of $15,000 one year from now if the opportunity cost of capital (discount rate) is 12% per year nominal annual rate compounded monthly?

 

 

8. What is the present value of an offer of $14,000 one year from now if the opportunity cost of capital (discount rate) is 11% per year nominal annual rate compounded monthly?

 

9. What is the future value of $20,000 which grows at a nominal annual interest rate of 12% per year, compounded monthly, for two years?

 

 

10. What is the future value of $25,000 which grows at a nominal annual interest rate of 11% per year, compounded monthly, for two years?